Basics
There are three different methods to perform straightness measurements with the HPI-3D device: Angular, Wollaston and 3D.
-
Used angular method in base straightness measurements (like optical autocollimator);
-
Use the Wollaston method to determine “movement in space” measurements. For example, to characterise the movement of a machine table or working tool;
-
Used 3D method for rapid estimation of “movement in space”. Similarly to Wollaston method but the measurement is HPI-3d performs in the three axes at once.
The main parameters of those methods are described in the Lasertex Technical Data below.
| Measurement | Range | Resolution | Accuracy |
|---|---|---|---|
| Straightness measurement (with angular optics) | 0 – 15 m | 0.01 µm (for 100 mm base) | ± 0.2 % |
| Straightness measurement (with Wollaston optics) | 0.3 – 9 m Vertical range up to ± 30 mm |
0.01 µm | ± 0.5 % x L µm |
| Straightness measurement (with 3D optics) | 0 – 6 m | 0.1 µm | ± ( 10 + 10 * L ) µm |
Angular method
Wollaston method
3D method
Angular method
 What optic to use?
What optic to use?
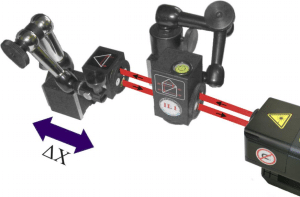
In the picture you can see the application of the angular measurement method. You can use HPI-3D with the angular optics. The laser emitter outputs two polarised laser beams: Horizontal (H) and Vertical (V). It is possible because beam spliter inside IK1 is set at the Brewster angle. Both beams are directed into the measurement path but are parallel shifted by 1’’ or 2’’ distance (depending on the version).
Measurement process
During the measurement process you alter the distance between optical elements. As a result the frequency of both beams changes according to the Doppler Effect. Keep in mind, the laser head does notice a movement only if there is a rotation of IK1 versus RK1. For instance, when there is difference in lengths of beam paths. User the measured distance to obtain either the rotation angle (pitch or yaw of the machine) or the vertical movement of the optical component (IK1 or RK1).
The laser head with angular optics is insensitive to linear movements.
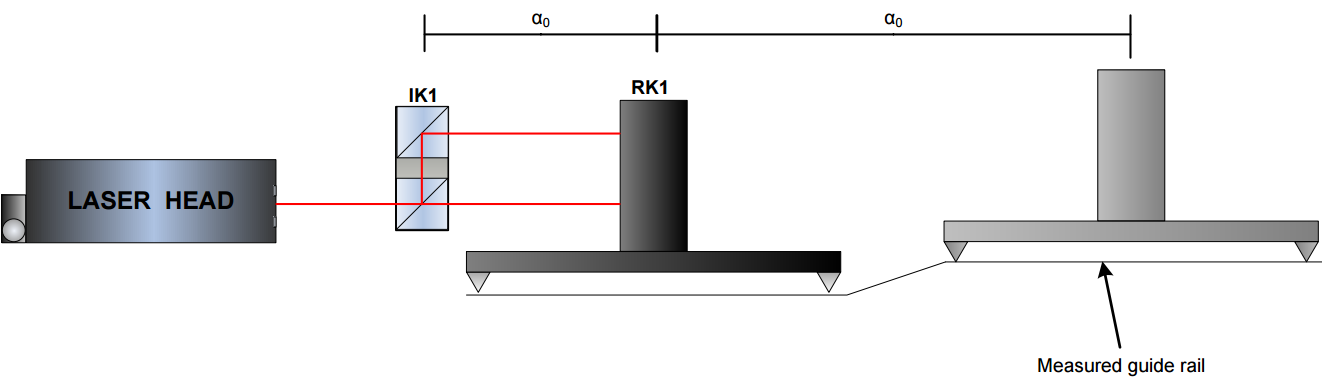
The picture schematically shows an RK1 on a carriage with all parameters important for calculation. To clarify the position of IK1 is treated as a reference. The meaning of the parameters are: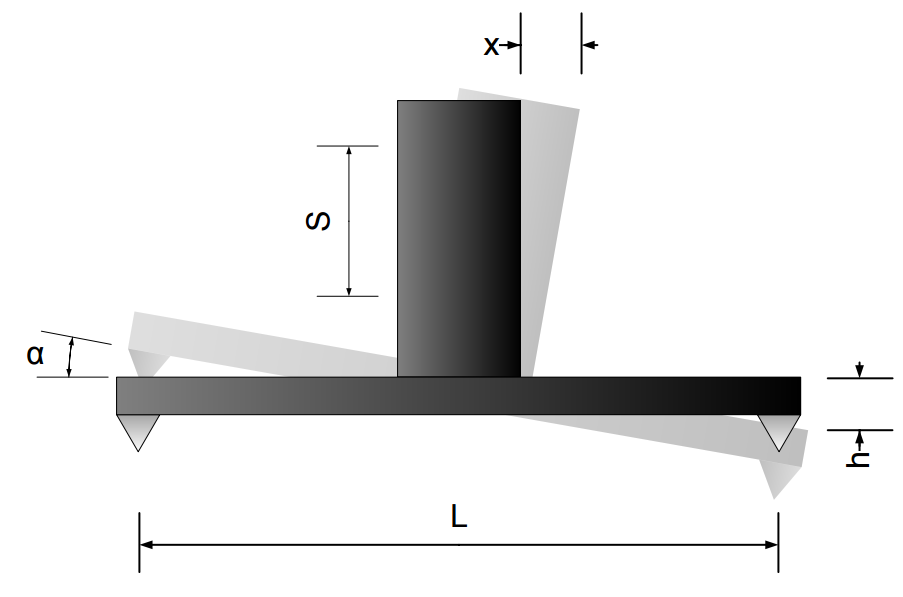
L – base length;
s – distance between beams on IK1 and RK1 elements;
x – distance measured by the Laser Head
α – angular rotation of RK1 element
h – difference in height between two measurement points
The Laser Head measures the parameter x. That is to say, the distance between beams s and the base length L must be set in the parameters of the HPI Software. Then the software can calculate the rotation angle α and the movement in the vertical direction h. Formula for the calculations:
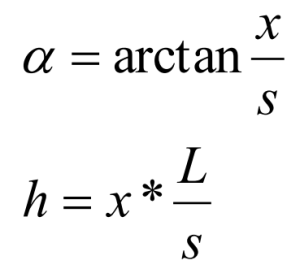
Application notes
Use the angular optics for the following type of measurements:
Measurement of pitch or yaw of a machine
Measurement of straightness of a machine bed
Measurement of small angles
Measurement of pitch or yaw of a machine and straightness of a machine bed
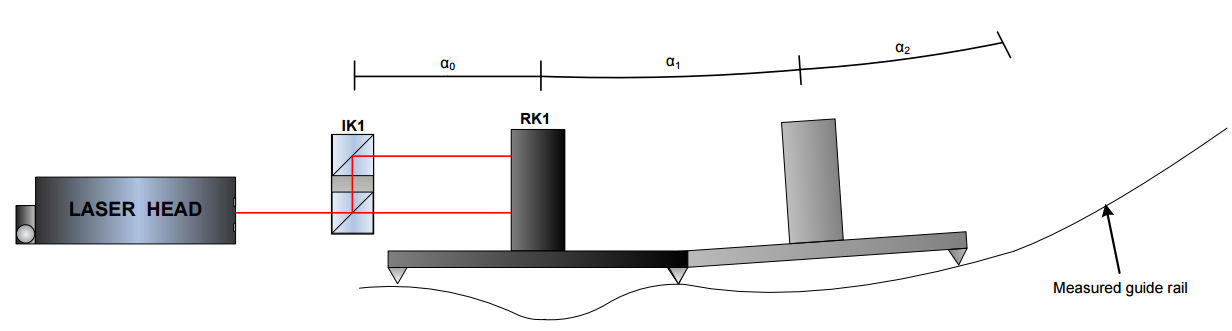 For the explanation of the first two applications see the picture. Move the RK1 prism assembly on a carriage over the measured guide rail. Meanwhile perform the measurements every 100 mm . The length of the carriage is usually 100mm to make it more convenient. In the same vein use formulas from previous chapter to calculate the angles (for pitch/yaw measurements) or the vertical translations (for straightness measurements).
For the explanation of the first two applications see the picture. Move the RK1 prism assembly on a carriage over the measured guide rail. Meanwhile perform the measurements every 100 mm . The length of the carriage is usually 100mm to make it more convenient. In the same vein use formulas from previous chapter to calculate the angles (for pitch/yaw measurements) or the vertical translations (for straightness measurements).
It is worth to notice, that such straightness measurement method requires proper choice of measurement points. That is to say, choosing points denser than the carriage size results in excessive values of the straightness errors. But the shape of the error is proper.
If you choose points too sparse it may effect both the shape and the value of the error as shown in the figure below. In this special case the measured distance between beams will not change, because of too sparse measurement points the laser will not notice the change in the shape of the guide rail!
Measurement of small angles
The measurement of small angles allows very accurate measurements of small rotations. However the following two conditions should be met:
1. measured angle is within ±5 degrees
2. distance between RK1 and the laser head does not change more than a few centimeters.
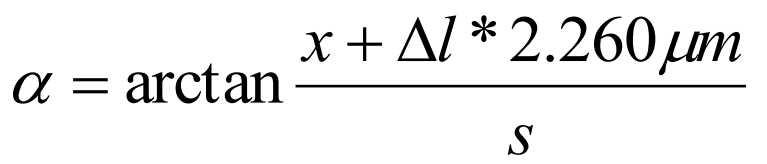 The second limitation comes from the heterodyne effect present in the HPI-3D laser. This effect influences the angle according to (Δl is the change of distance between the laser and RK1 during measurements)
The second limitation comes from the heterodyne effect present in the HPI-3D laser. This effect influences the angle according to (Δl is the change of distance between the laser and RK1 during measurements)
Wollaston method
Wollaston optics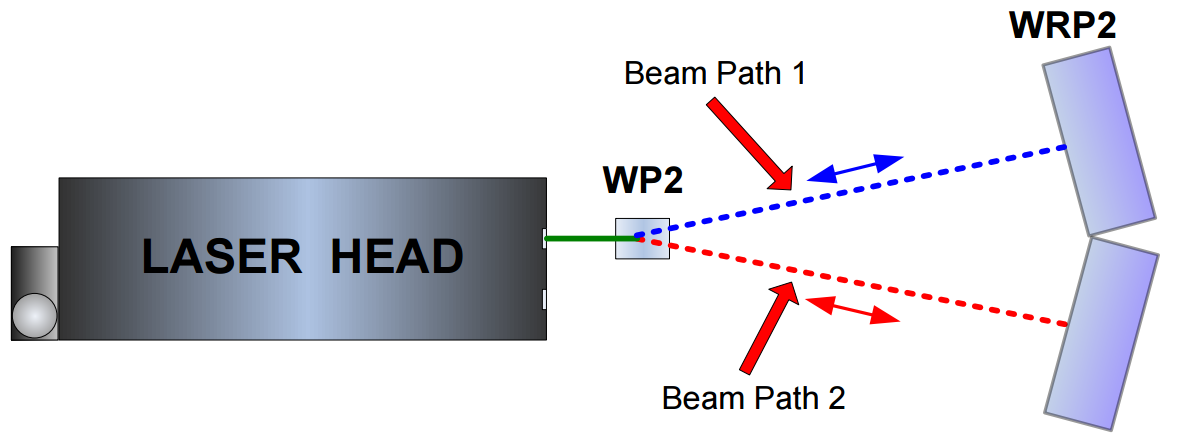
Another way of measuring straightness, parallelism and squareness with the laser interferometer requires the use of Wollaston type optics. The optics consist of two elements: Wollaston polarizing prism WP2 and a paired reflector WRP2 – see figure below. The laser beam, consisting of two perpendicular polarizations, is split by the WP2 element into two beams. The beams are leaving the WP2 at a certain angle and then, after being reflected back by the reflector WRP2 are returning to the laser head. The laser measures the difference between beams’ paths lengths.
Prism construction
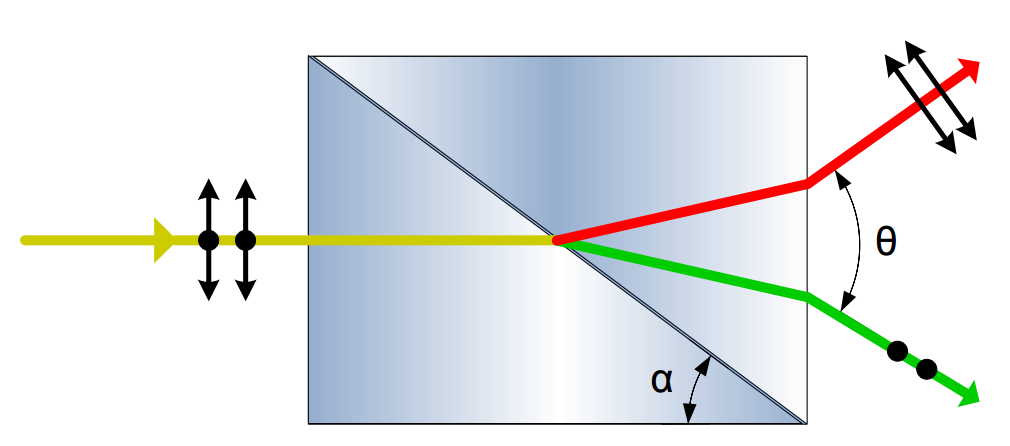
In the figure you can see the the WP2 element operation explanation. This prism is constructed of two birefringent triangle prisms cemented together. Both prisms are built from the same material but their ordinary and extraordinary axes are perpendicular to each other, i.e. refraction coefficient of the ordinary axis of the left prism nol equals to the coefficient value of the extraordinary axis of the right prism ner.
Because of this the orthogonally polarized laser beams entering the Wollaston element are deflected at different angles on the middle boundary layer and on the right boundary layer. This behavior can be easily proven with the use of the Snell’s law. The angle between the exiting beams is often denoted as Θ.
 Unlike in the angular optics the distance between beams are changing with distance, thus making the construction of the reflecting element difficult. In the figures below there is shown the construction of the reflection element for the Wollaston optics WRP2. It consists of two special glass prisms glued very precisely at 180-Θ angle. The prisms used in the WRP2 in y axis reflect the beam with ½’’ translation (like the retroreflector RL1). In the x axis the beam is reflected with no translation (like in a mirror).
Unlike in the angular optics the distance between beams are changing with distance, thus making the construction of the reflecting element difficult. In the figures below there is shown the construction of the reflection element for the Wollaston optics WRP2. It consists of two special glass prisms glued very precisely at 180-Θ angle. The prisms used in the WRP2 in y axis reflect the beam with ½’’ translation (like the retroreflector RL1). In the x axis the beam is reflected with no translation (like in a mirror).
The laser head with Wollaston optics is sensitive to angular movements of the reflector!
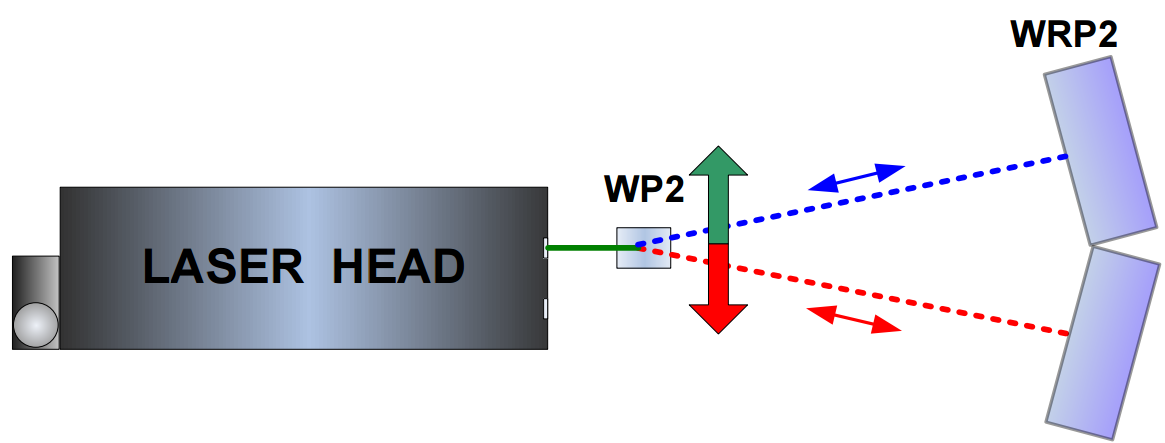 The use of Wollaston optics makes possible the measurement of relative movement of WP2 element in the axis perpendicular to the laser beam. As it is shown in the figure below the measurements are possible ONLY with the WP2 movement.
The use of Wollaston optics makes possible the measurement of relative movement of WP2 element in the axis perpendicular to the laser beam. As it is shown in the figure below the measurements are possible ONLY with the WP2 movement.
Because of the sensitivity of the laser readout on the angular movement of the WRP2 it is important that during measurements the WRP2 element is neither touched nor moved.
Application notes
Although it is possible to measure the straightness either with movement of the WP2 or WRP2 element but there are certain differences. The WRP2 this element should be stationary during measurement (i.e. should not be moved along the laser beam). As the WRP2 behaves in one of the axis like a mirror thus any angular movement of the WRP2 in this axis may result in the laser beam not returning to the laser head and will influence significantly the measurement results!
There are no such problems when the WP2 is moved instead. The only disadvantage is the smaller measurement range. WP2 can be moved ±2mm while maximal measurement range of the WRP2 is ±30mm (but only when the distance between WP2and WRP2 is 4.5 m).


3D method
 The HPI-3D laser head is capable of detecting the position of the returning beam. The position of the returning beam changes with the movement of the retroreflector RL1 perpendicular to the laser beam axis. This phenomena for one axis is shown in the figure below. The beam returning from the linear interferometer IL1 is treated as a reference while the beam reflected by RL1 as measuring beam. The laser simultaneously registers information about the changes of position of an optical component in both axes perpendicular to the laser beam.
The HPI-3D laser head is capable of detecting the position of the returning beam. The position of the returning beam changes with the movement of the retroreflector RL1 perpendicular to the laser beam axis. This phenomena for one axis is shown in the figure below. The beam returning from the linear interferometer IL1 is treated as a reference while the beam reflected by RL1 as measuring beam. The laser simultaneously registers information about the changes of position of an optical component in both axes perpendicular to the laser beam.
The measured position is then used either for precise control of the laser beam path alignment or for the straightness, squareness or parallelism measurements. The 3D measurement returns absolute values of the beam position. This is different from the main, interferometric measurement axis where obtained results are incremental.
Application notes
The 3D option can be used for rapid estimation of straightness simultaneously in two axes but with some limitations resulting from physical nature of the measurements.
Unlike in all interferometric measurements, the laser head takes active part in the measurements, i.e. its position and its vibrations influences the measurement results. For this reason it is important to avoid using the tripod stand and to fix the laser head directly on the measured machine.
The 3D measurement bases on the position of the returning beam on the position sensitive device. Thus it is important that the beam stays within the measurement range of the device, i.e. ±1 mm. Using 3D option outside this range would produce unreliable results.
Similarly to all laser based straightness measurements the air turbulences have an influence on the results. Small wandering of the laser beam can be accommodated by the signal processing circuit inside the laser with the change of averaging time (see Software Description for more details). If the air movements are too large – i.e. when the beam returning to the laser wanders outside ±1 mm window – then the results of the 3D measurements may become unusable. In such situation either some shielding from the air movement or a fan forcing the air movement have to be used. The problem with air turbulences is more troublesome for larger distances between the laser head and RL1 element.